Exam 1 study guide | Microeconomics

Capitalism + governments and institutions

You should understand…

…the components of the capitalist economic system: private property, markets, and firms
…what happens when any of these components gets distorted
…what makes public goods different from regular goods (see public goods game)
…what institutions are and how they coordinate action
…what GDP is, what it measures, what it doesn’t measure, what problems there are with it, what alternatives there are for it, and why it continues to be popular
…the difference between real and nominal values (and why we care)
…what a price index is
…what purchasing power parity (PPP) is (and also what the Big Mac Index is)
…the downsides of capitalism (inequality + environmental damage)
…why not everything should be a market
…why large groups suffer from free riding and how they work to behave like small groups
…how small factions threaten democracy, but also how they enable it
…how voting can suffer from failures (Condorcet’s paradox)

Important formulas:

Adjusting for inflation:

\[ \text{Real} = \frac{\text{Nominal}}{\text{Price Index / 100}} \]
Percent change:

\[ \text{% change} = \frac{\text{New} - \text{Old}}{\text{Old}} \]

or

\[ \text{% change} = \frac{\text{Current} - \text{Previous}}{\text{Previous}} \]
Compound annual growth rate (CAGR); periodic method (this assumes interest is compounded once a year; this is the harder method and you don’t really need to use it):

\[ r = \exp(\frac{\ln(\frac{\text{Price index}_{\text{new}}}{\text{Price index}_{\text{old}}})}{t}) - 1 \]
Compound annual growth rate (CAGR): continuous method (this assumes interest is compounded continuously; this is the easier method and you should generally use this):

\[ r = \frac{\ln(\frac{\text{Price index}_{\text{new}}}{\text{Price index}_{\text{old}}})}{t} \]

Guides:

Inflation and change

Other helpful resources:

CPI calculator

Social interactions, economic outcomes, and incentives

You should understand…

…that perfectly rational individual behavior can create irrational and inferior social outcomes
…how to use game theory to analyze social interactions. In particular, you should be able to define the following: game, zero-sum, Pareto efficiency, Nash equilibrium, pure strategy, mixed strategy, dominant strategy
…what social dilemmas, collective action problems, and tragedies of the commons are
…the difference between a stag hunt game and a prisoners dilemma game, why that difference is important, and why stag hunts are possibly a better metaphor for social dilemmas
…what factors prevent individuals from cooperating, such as uneven payoffs, lack of assurance, preference falsification, dishonesty, and selfishness
…how to fix collective action problems with altruism, repetition and iteration, infinitization, punishment, norms, and institutions
…how incentives can get crowded out and distorted when extrinsic rewards or punishments replace intrinsic motivation (i.e. don’t marketize important social relationships; pay enough or don’t pay at all)

Guides:

Game theory

Other helpful resources:

Fairness and efficiency

You should understand…

…the difference between Pareto efficiency and fairness
…why Pareto efficiency is not necessarily the best standard for measuring the success of a policy
…how we can measure fairness with substantive standards, procedural standards, and Rawlsian standards
…how cultural perceptions of luck and fairness shape public policy
…how ideas of efficiency and fairness apply to international trade
…how public policy can be used to change the payoffs in games (e.g. making it more expensive to use water and deplete public goods)
…what elasticity measures (i.e. what it means for something to be inelastic vs. elastic)
…why good public policies should be a Nash equilibrium
…the difference between absolute and comparative advantage and how there can still be gains from trade if a part doesn’t have absolute advantage in a product

Guides:

Absolute and comparative advantage

Work, wellbeing, and scarcity

You should understand…

…what opportunity costs are and how they influence decision making
…how to draw a budget line and what budget lines mean
…how utility is measured and what indifference curves are
…the difference between the marginal rate of substitution (slope of the indifference curve) and the marginal rate of transformation (slope of the feasible frontier)
…what it means when marginal product and marginal utility diminish
…how to find the utility-maximizing level of consumption given preferences and budget constraints
…the difference between normal and inferior goods
…what income effects and substitution effects are and how they’re related to government policies

Important formulas:

All the ways marginal utility (or marginal rate of substitution) can be written:

\[ MRS = \frac{dy}{dx} = \frac{\Delta y}{\Delta x} = \frac{\text{Price}_x}{\text{Price}_y} = \frac{MU_x}{MU_y} = \frac{\partial u / \partial x}{\partial u / \partial y} \]

Guides:

Other helpful resources:

The firm

You should understand…

…how the decision-making structures of firms and markets are different
…that perfectly complete contracts are difficult (if not impossible) to create
…what happens when there are incomplete contracts
…what a principal-agent problem is
…adverse selection
…moral hazard
…how firms can use the labor discipline model to induce higher worker effort
…why involuntary unemployment is necessary

Firms and markets

You should understand…

…how demand curves are derived from consumer willingness to pay
…the difference between fixed costs and variable costs
…how to calculate total cost, total revenue, average fixed costs, average variable costs, marginal cost, marginal revenue, and maximum profit
…that maximum profit occurs where marginal revenue is equal to marginal cost (\(MR = MC\))
…that socially optimal quantity occurs when the demand is equal to the marginal cost (\(\text{demand} = MC\))
…how to calculate elasticity of demand (\(-\frac{\Delta Q}{\Delta P} \times \frac{P}{Q}\))
…what elasticity measures and why it is important in public policy and administration
…how a single demand curve can have an overall elasticity and different elasticities at each point
…economies of scale, diseconomies of scale, economies of agglomeration, network effects, and the difference between short-run and long-run costs
…that market equilibria (i.e. optimal price and quantity) occur at the intersection of supply and demand curves
…how government-imposed price floors and price ceilings distort market-clearing equilibria
…and be able to identify the differences between changes in supply/demand and changes in quantity supplied/demanded
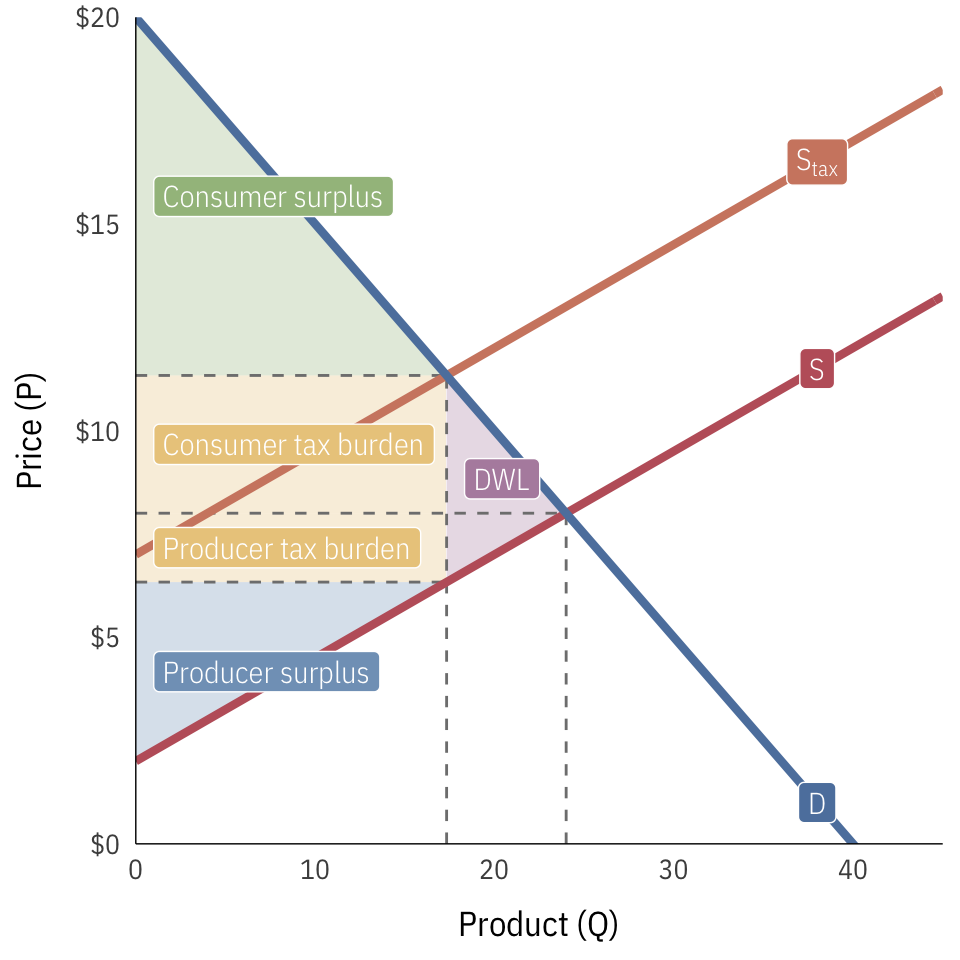
…what consumer and producer surplus represent
…the relationship between elasticity of supply and/or demand and the size of consumer and producer surplus
…how taxes impose deadweight loss on society
…how the burden of taxes depends on the elasticity of supply and/or demand
…why governments tax and the philosophical and ethical principles behind who should bear the burden of taxes
…the difference between price-taking and price-making
…how firms try to gain market power, including monopolies, branding, cost controls, regulation, and switching costs
…why firms try to gain market power
…why firms want to price discriminate
…the consequences of monopolistic production (lower Q and higher P than what would happen under perfect competition; deadweight loss)
…how governments can regulate monopolies
…why natural monopolies exist and how governments can induce them to produce at socially optimal levels
…how firms need to be somewhat anti-competitive and anti-capitalist in order to maximize profits, innovate, and (essentially) be more competitive and capitalist

Guides

Important formulas:

Demand:

\[ P = aQ + b \]
Total cost:

\[ \begin{aligned} TC = TFC + TVC \\ \text{or a formula using } Q \text{, like} \\ TC = aQ^2 + b \end{aligned} \]
Average cost:

\[ AC = \frac{TC}{Q} \]
Marginal cost:

\[ \begin{aligned} MC &= \frac{\Delta TC}{\Delta Q} \\ &\text{or} \\ MC &= \text{First derivative of TC} \\ &= 2aQ \text{ (if } TC = aQ^2 + b) \end{aligned} \]
Total revenue:

\[ \begin{aligned} TR &= PQ \\ &\text{or} \\ TR &= (aQ + b)Q \\ &= aQ^2 + bQ \end{aligned} \]
Average revenue:

\[ AR = \frac{TR}{Q} \]
Marginal revenue:

\[ \begin{aligned} MR &= \frac{\Delta TR}{\Delta Q} \\ &\text{or} \\ MR &= \text{First derivative of TR} \\ &= 2aQ + b \text{ (if } TR = aQ^2 + bQ) \end{aligned} \]
Maximum profit:

\[ max(\pi): MC = MR \]
Price elasticity of demand (see this guide of how to get to \(- \frac{\Delta Q}{\Delta P} \times \frac{P}{Q}\)):

\[ \varepsilon = -\frac{\% \text{ change in quantity demand}}{\% \text{ change in price}} = - \frac{\Delta Q}{\Delta P} \times \frac{P}{Q} \]

Important graphs:

Consumer surplus, producer surplus, tax revenues, tax burdens, and deadweight loss (use algebra and geometry to figure out the areas of the triangles (\(\frac{1}{2} \times b \times h\)) and rectangles (\(l \times w\))):

Helpful resources:

Derivatives of Exponential Functions (how to calculate derivatives quickly)
Jason Welker, “Natural Monopoly and the Need for Government Regulation”